“On the shoulders of giant numbers”
 http://www.allergrootste.com/big/book/ch1/ch1_6.html  bigΨ

§1.6.1. Egyptian hieroglyph of a million (or not yet?)

The human ability to express large quantities in a terse manner has evolved from Egyptian hieroglyphs via Indian decimal numbers all the way to modern day operator-style exponentiation. Using only decimal signs for the sake of comparison, we can show how the word length for writing numbers gets shorter in the course of history.

Of course the numerals of the Egyptians were different, but already they used powers of 10 as countable units in a primitive number system without multiplication by digits.
The signs for 1 10 100 1000 10000 100000 1000000 appear to be five thousand petalled lotus years old, while some are inscribed on a ceremonial mace-head of the possessive conqueror Pharaoh Narmer (1st dynasty).

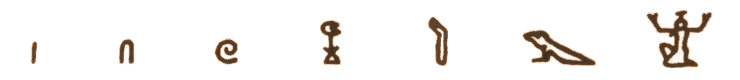
The hieroglyph of the numeral unit on the right – what Georges Ifrah calls a kneeling genie (holding up the sky) – is known to signify the megalithic figure of a million 10^6, as well as infinity.
The sign of the sun for 10^7 that we find in Gheverghese Joseph is less well documented and of a later date.

Now it might be that the 3100 BC figure of a kneeling person was misinterpreted to stand for a million by Egyptologists as well as by the Egyptians of the 2nd millennium BC who adopted it as such.
Ifrah notices that, for this sign on the mace-head to be a numeral, the usual order of the hieroglyphs must be jumbled up. Surely, considering the count of 400,000 bulls in Pharaoh's war bounty, a captured 1,422,000 goats is a ridiculously precise number!

We suggest that the figure later in use as a million, on Narmer's mace-head still represents a subjugated cowboy (+cowgirls?), one of 2000+ herders who were needed to take care of the herds of the cows and some 420,000 goats. They clearly have their hands free, while the 120,000 manly prisoners of war sit with their arms tied behind their back.

§1.6.2. Greek powers of Archimedes (or not quite?)

The Greeks also used multiples of 1,10,100,1000 in their number system, each with 10 different letter signs. Writing only four letters all whole numbers up to a myriad or 10000 can be formed. The same is true in our decimal system, but with all the variation in Greek letters and auxiliary signs multiplication becomes troublesome.
In expressions such as ,ατλα.,εσιδ = 13315214 the number of myriads is added to a smaller number by a dot (in an example of Diophantus c.3d century AD). Then myriad myriads or 10^8 could be named but not written.

Anyhow, the main topic of interest for the ancient Greeks was geometry and trigonometry and there calculations rely on ratios of lines, angles, areas and volumes.
Generously pursuing mathematics for its own virtue Euclid (c.300-260 BC) wrote his Elements, the start of modern mathematics. Euclid's foundation of geometry was rock solid. Attempts to prove his postulate for non-parallel lines from other axioms failed and instead gave rise to non-Euclidean geometry in the 19th century.

With Archimedes of Syracuse (c.287-212 BC) the dispute over the scale of the physical universe versus the capacity of arithmetical numbers was decided once and for all in favour of pure mathematics.
In his Sand number article Archimedes derives an upper bound for the number of sand grains 10^51 that fit inside the Greek universe (the sphere where the sun revolves around the earth) from personal measurements and a clever geometrical proof. He also discusses Aristarchus of Samos' heliocentric theory where the sphere of fixed stars has a diameter that is 10000 times greater, but calculates it contains no more than 10^63 sand grains.

Archimedes' system for large numbers is divided into 10^8 periods, each period subdivided in 10^8 orders, each order consisting of 10^8 numbers of units, each unit a copy of the highest number of the previous order.

1. Numbers from 1 up to (10^8)^(10^8) in the 1st period:
   • Call the numbers from 1 to a myriad myriads (10^8) numbers of the 1st order
   • Then let 10^8 be unit of the 2nd order numbers up to (10^8)×(10^8)
   • This 10^16 unit of 3d order numbers ending with (10^8)^3, and so on ...
   • Until the 10^8th order numbers will end with (10^8)^^2 the 1st period.
2. Numbers from P = 10^(8×10^8) up to P^2 in the 2nd period:
   • Call the numbers from unit P to P×10^8 of the 1st order in the 2nd period
   • Let P×10^8 be the unit of its 2nd order up to P×(10^8)^2, and so on ...
   • Until its 10^8th order numbers end with P×(10^8)^(10^8) the 2nd period.
3. Rest from P^2 up to 10^(8×10^16) in the 10^8th and last period:
   • The 3d period then will cover the numbers up to P^3
   • The 4th period the numbers up to P^4, and so on ...
   • Until the 10^8th order in the 10^8th period ends with P^(10^8)
   • Last octad (10^8)^(10^8)^2 = 10^(8×10^16)

In this system natural numbers are precisely expressed (and uniquely, without the myriad myriads terms) as the total of the numbers of different units. But usually an approximation is more practical, Archimedes recognized this and divided up the orders of his system in octads, with as terms just the order's unit and the next 7 powers of ten.
So the quantity 10^63 = 10^(7+8×7) = 10^7×(10^8)^7 of sand grains is expressed as a thousand myriad units of the eighth order – serving to illustrate how small this first period number is, compared to those in the later periods of Archimedes' system.

Archimedes wrote a series of octads with indices from A1 to A8 expressing the numbers 1 to 10^7, and defined his law of indices as Am*An = Am+n-1 much like our law of exponents a^m×aⁿ = a^m+n but not quite!
Because index value 0 is missing, this hides the fact that a⁰ = 1 and the second law Am^n = Am*n-n+1 will become less obvious. Archimedes multiplied two octads by adding the distance of their indices from base index A1 and in this context the multiplication of indices escapes from view.
With the luxury of an exponential operator ^ we now define the power laws.

In this chapter we met the largest number 10^8×1016 of Archimedes and hence of ancient Greece.

Although Archimedes' system covers all whole numbers up to this limit, a binary number this size that's randomly chosen would consume 30213 TB of computer disk space.
Our universe has expanded since the time of Aristarchus, nowadays (2010) it is estimated to contain 3E23 stars – a number bigger than the sand grains on all the world's beaches, but still less than the sands in the Sahara desert.

§1.6.3. Indian decimal expansions (oh really?)

About that time in India the void (Sanskrit: šünyatä = emptiness) got a good press and eventually was rewarded (circa 650 AD) with its own numeric sign 0 for no cipher. This nought had the practical use of filling in the empty spaces in decimal numbers such as 108 but came too late for the early religious devotees who used large numbers to explain the greatness of their Gods or to count a multitude of enlightened beings.

Centuries after the historical Buddha was gone, in the Lalitavistara Sutra a literary Buddha explains a number system to the mathematician Arjuna. Starting from a koti 10^7 moving in multiples of 100 up to 10^53 (tallakshana = a mark), calling every odd power by its own name.
Building on this first kotisatottara numeration follow 8 numerations of the powers up to 10^(7+46×9) provided these are listed as before (something of a modern tradition). The way the sands of Ganges rivers come into the equation makes this interpretation very awkward, but we don't have any better, so we'll follow up on it.

The last number 10^421 (uttaraparamânurajahpraveša) is often cited as a Sutra record, but if numerations line up as presumed, it would mark the initial atom of a highest numeration ending with 108470495616000 atoms in a yojana. Even bigger is the mass of a yojana, calculated at about 1E28 atoms. When a world of four continents contains 34000 yojana and there are 1E9 such worlds, the total mass would be about 3.4E41 atoms, equal to a record 3.4E462 in number (the physical entity translates to a pure Big number).
Assuming that all 30 realms of the three thousand great thousands of worlds in the Lalitavistara are quantatively similar (a tall order), and given that the Buddha declares their universal mass as incalculable, our fuzzy Sutra record 1E464 sets a new bound on the asamkhyeya, the number the Indians conjectured to be at infinity.

With this lesson in enumeration the young Buddha, prince of Šâkyas, passes his maths test. But still an error went unnoticed.
Usually a three-thousand-great-thousandfold-world counts a billion, a 1000×1000×1000 worlds, times 3 to extend this cube over the trinity of desire, formation and formlessness. But the Lalitavistara lists 30 realms, each with 100 kotis of worlds. So either a koti is a million (instead of ten million) or the Sutra writers didn't have the skill to compare such numbers. Here we've assumed the latter.

Large Indian numbers can be lengthy compound words, or in a list mostly imagined names, where they were recited as mantras, perhaps meant to develop one's arithmetical prowess. Never the series of decimal zeros (made in India) modern man expects here. Zero was not a word yet and the concept of a 1 followed by a row of empty 0.. didn't ring a (mindfulness) bell, which explains the error above. Maybe the American Googols were an invention after all?!

Anyhow, it happened that the literary Buddha dried out and the mahâyâna (Great Vehicle) buddhists developed a big thirst for stupendous baroque visions of universal Buddhas. These godlike creatures inspired lengthy arrays of numbers to count their manifold virtues and huge hosts of followers, in a library packed with scriptures of which the most renowned are the Lotus Sutra and the Flower Ornament Sutra.